УДК 621.317.33
В.В. Поляков, А.В. Егоров Процессы переноса в пористых
металлах
Закономерности процессов переноса в неоднородных конденсированных средах сложным образом зависят от структуры материала и соответствующих механизмов рассеяния [1]. Специфическим классом неоднородных материалов являются пористые металлы, выступающие в качестве предельного случая гетерофазной среды с максимально различающимися свойствами
составляющих компонентов — металлического каркаса и пор [2]. Это делает пористые металлы важным модельным объектом для анализа фундаментальных закономерностей поведения конденсированных сред. В настоящей работе на основе экспериментального исследования влияния пористости на электропроводность, теплопроводность и вязкость выясняются особенности физических механизмов переноса в пористых металлах и формируется теоретический подход, позволяющий с единых позиций рассчитать характеристики переноса и описать их особенности.
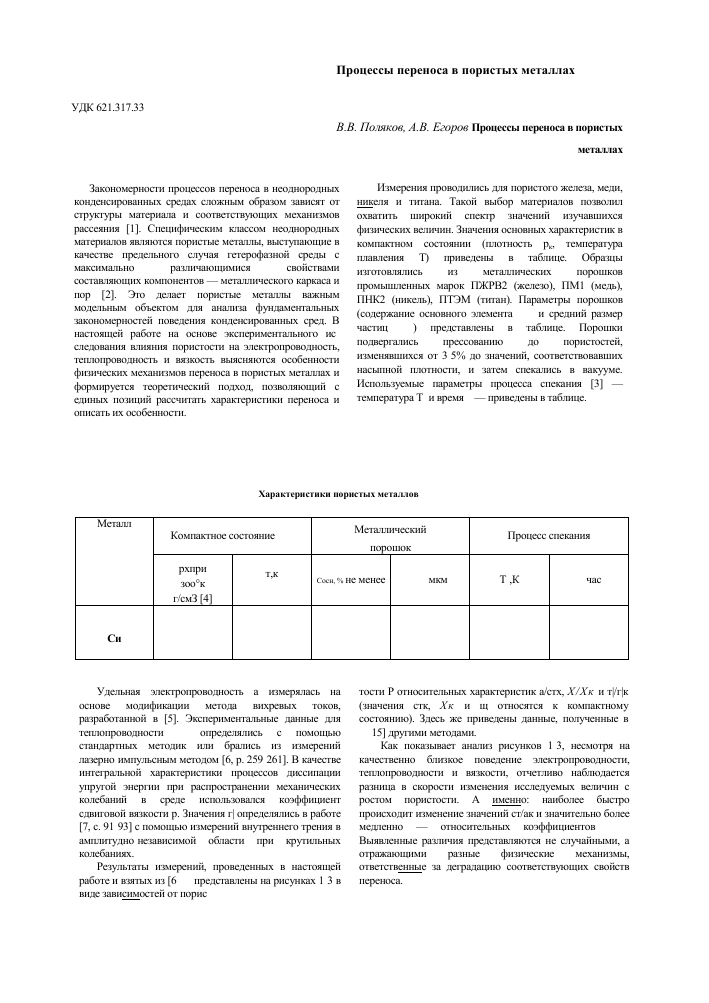
Измерения проводились для пористого железа, меди, никеля и титана. Такой выбор материалов позволил охватить широкий спектр значений изучавшихся физических величин. Значения основных характеристик в компактном состоянии (плотность р^, температура плавления Т) приведены в таблице. Образцы изготовлялись из металлических порошков промышленных марок ПЖРВ2 (железо), ПМ1 (медь), ПНК2 (никель), ПТЭМ (титан). Параметры порошков (содержание основного элемента С05П и средний размер частиц К представлены в таблице. Порошки подвергались прессованию до пористостей, изменявшихся от 3-5% до значений, соответствовавших насыпной плотности, и затем спекались в вакууме. Используемые параметры процесса спекания [3] — температура Т8 и время ^ — приведены в таблице.
Характеристики пористых металлов
Металл Компактное состояние Металлический Процесс спекания
порошок
рхпри зоо°к т,к [4] Сосн, % не менее Rg, мкм Т5,К ts, час
г/смЗ [41
Ft Ni Си Ti 8,86 8,96 8,92 4,50 1811 1728 1357 1941 99,5 99,7 99,5 99,0 80 30 25 30 1520 1590 1170 1370 2,5 2,5 3,5 2,5
Удельная электропроводность а измерялась на основе модификации метода вихревых токов, разработанной в [5]. Экспериментальные данные для теплопроводности X определялись с помощью стандартных методик или брались из измерений лазерно-импульсным методом [6, р. 259-261]. В качестве интегральной характеристики процессов диссипации упругой энергии при распространении механических колебаний в среде использовался коэффициент сдвиговой вязкости р. Значения г| определялись в работе [7, с. 91-93] с помощью измерений внутреннего трения в амплитудно-независимой области при крутильных колебаниях.
Результаты измерений, проведенных в настоящей работе и взятых из [6-8], представлены на рисунках 1-3 в виде зависимостей от порис
тости Р относительных характеристик а/стх, Х/Хк и т|/г|к (значения стк, Хк и щ относятся к компактному состоянию). Здесь же приведены данные, полученные в [9-15] другими методами.
Как показывает анализ рисунков 1-3, несмотря на качественно близкое поведение электропроводности, теплопроводности и вязкости, отчетливо наблюдается разница в скорости изменения исследуемых величин с ростом пористости. А именно: наиболее быстро происходит изменение значений ст/ак и значительно более медленно — относительных коэффициентов 1;|/г|к. Выявленные различия представляются не случайными, а отражающими разные физические механизмы, ответственные за деградацию соответствующих свойств переноса.
Рис. 1. Зависимость относительной удельной электропроводности от пористости: Ке: + - настоящие измерения, X - измерения [8], * - из
[9]; Си: О - из [8], V - из [10], Д - из [11]; N1: • - из [8]; Л: ▼ - настоящие измерения, А - из [12]
Рис. 3. Зависимость относительной сдвиговой вязкости Ке - из [7]
При моделировании процессов переноса предполагали, что соответствующий «поток» (электрический ток, тепловой поток и т.д.) переносится в одном направлении параллельно плоскостям ячейки. Такой «поток» огибает пору или обрывается на ней в зависимости от геометрических параметров структуры и характеристик конкретного процесса рассеяния. Удобно ввести размер X области за порой, не достигаемой для «потока». Моделируя прохождение потока через структурные элемента ячейки, получали различные схемы соединения проводящих элементов. Определяя общее сопротивление такой системы элементов и приравнивая его к номинальному сопротивлению ячейки, находили эффективную проводимость. Функциональная зависимость для относительных эффективных характеристик пористой среды в случае изолированных пор имела следующий вид:
Рис. 2. Зависимость относительной удельной теплопроводности от пористости: Си: + - из [6]; Ре: О - из [6] и настоящие измерения, V -
из [13], Д - из [14], П - из [15]; N1: • - из [10]; Т1: ▼ - настоящие измерения, А - из [12]
Для моделирования структуры использовался метод элементарной ячейки [2]. Согласно этому методу реальная пористая среда заменялась идеализированной структурой, обладавшей дальним порядком. В такой структуре возможно выделение ячейки, определяемые физические характеристики которой принимаются за искомые эффективные свойства среды. В случае материала с примерно равноосными порами справедливо положение о малом влиянии формы пор на свойства проводимости [16]. Это позволило выбирать форму ячейки, наиболее удобную для конкретной задачи. В настоящей работе использовались ячейки с кубической симметрией [8].
/0) _
/2(р) + т + /г4Р)х/г([)
где/(Р) — = Р . Для сообщающих»
пор получали аналогичное выражение:
рт
П + А(Р)!1-А(Р¥
1-/2(Р)+2/22(Р)+2/22(Р)х/г '
[2]
где функция/2(Р) — /Я находится по знач< ниям Р с помощью уравнения
3/22(Р)-2/3(Р) = Р.
Для расчета эффективных свойств необходимо задание функции х(г) , которая бралась в виде [8'
Яс, г > Яс(//1 — I)1, х(Г) = •
(3)
/(/г'-1), г<Яс(/,г1-1у1>1 = \,2,
где параметр Яс характеризовал особенности рассеяния «потока» в пористой среде.
В пористой среде при значениях Р, превышающих порог перколяции Р0 [17, с. 401-435], одновременно присутствуют как изолированные, так и сообщающиеся поры. Их вклады согласно [18, с. 81-85] можно описать с помощью функции а(Р):
1Р о
() [PJP,P>P,. (4)
Это позволяет объединить уравнения (1) и (2), представив их в виде, охватывающем весь возможный интервал пористостей:
(5)
Ансамбль пор в реальном материале может содержать пустоты, существенно различающиеся по величине. Это требует обобщения на случай полидисперсной пористой среды. Пусть распределение пор по размерам задается дифференциальной функцией распределения (p [r,r,D), где Г иО — средние размер и дисперсия пор. Обобщением моно дисперсного описания является следующее выражение для эффективного свойства:
F(P,r,D) = I F(P,r)<p(r,r,D)dr.
Полученные выражения использовались для расчетов характеристик переноса. В качестве критической пористости использовалось значение Р0= 0,07. Функции (p(r,7,D) задавались в виде нормального распределения с наложением, параметры 7 и D оценивались по данным металлографического анализа шлифов.
При вычислении относительной электропроводности сг/ ак = Fe (P ,гпараметр Я принимался равным среднему размеру частиц ^, что отражало доминирующую роль меж- частичных пор в процессах рассеяния.
Для теоретического анализа теплопроводности необходимо учесть различия в физических механизмах рассеяния при тепло- и электропереносе. Теплопроводность А пористой среды определяется поведением как электронного вклада Д (преобладающего для металлов), так и решеточного члена А*. А.—Ае+А§.
Относительная электронная составляющая может быть описана той же функцией
F '{P ,7 ^) , что использовалась в случае электропроводности. Аналогичная зависимость F*(P ,7 ^) для решеточного вклада должна иметь такой же функциональный вид, но с иным значением параметра Яс, что отражает различие во влиянии пористости на перенос свободных электронов и колебания решетки. В результате для относительной теплопроводности получаем
д/4 = 7 Fe(P,7,D) + (1 - Y)F 0{P,7,D), (7)
где коэффициент у определяет долю электронной составляющей у = 4 / 4 •
При расчетах теплопроводности использовались значения у для неупорядоченных компактных металлов: у » 0,8 [19]. За величину Яс в решеточном члене принимался размер дефектной области, равный среднему размеру субзерен.
Вычисления относительной сдвиговой вязкости, тЦ1)к — 7"{К,r,V), проводились с теми же значениями параметра Яс, которые применялись для решеточного вклада в теплопроводность. Это отражало особенности коллективных неупругих эффектов рассеяния механической энергии при упругих колебаниях. Результаты расчетов характеристик переноса приведены на рисунках 1 -3 в виде кривых. Как видно из рисунков, теоретические кривые согласуются с экспериментом, при этом они правильно передают сдвиг вправо «коридора» экспериментальных точек при переходе от электропроводности к теплопроводности и вязкости.
Проведенное комплексное исследование показало, что при анализе закономерностей формирования свойств переноса в пористых металлических материалах необходимо учитывать различия в физических механизмах, определяющих протекание
соответствующих процессов. Изложенный в работе теоретический подход позволил учесть эти различия и провести адекватное описание влияния структуры на характеристики переноса.
Литература
1. Займан Д. Модели беспорядка. М., 1982.
2. Дульнев Г.Н., Новиков В.В. Процессы пере- носав неоднородных средах. JL, 1991.
3. Гегузин Я.Е. Физика спекания. М., 1984.
4. Свойства элементов. Ч. 1. Физические свойства: Справочник. М., 1976.
5. Поляков В.В., Егоров А.В. Устройство для вихретокового контроля электромагнитных параметров ферромагнитных материалов // Патент РФ №2027179 от 16.06.92. G01N27/90. Опубл. в бюл. №2 от 20.01.95.
6. Polyakov V.V., Utemesov М.А., Egorov A.V. Dependence of thermophysics properties of metals upon porosity // R.J. of Engin. Thermophys. 1995. № 3.
7. Поляков B.B., Алексеев A.H. Зависимость внутреннего трения и упругих характеристик пористого железа от пористости // Порошковая металлургия. 1994. № 34.
8. Поляков В.В., Егоров А.В. Зависимость электропроводности пористых металлов от структуры // Теплофизика и аэромеханика. 1994. Т. 1. № 2.
9. Роман О.В., Скороход В.В., Фридман Г.Р. Ультразвуковой резистромегрический контроль в порошковой металлургии. Минск, 1989.
10. Ondracek G., Nikolopoulos P. The correlation between properties and porosity of sintered materials // Proc. Powder Metall. Conf. P/M 82. Florence, 1982.
11. Витязь П.А., Капцевич В.М., Шелег В.К. По
ристые порошковые материалы и изделия из них. Минск, 1987.
12. Малько П.И., Аренсбургер Д.С., Пугин B.C., Немченко В.Ф., Львов С.Н. Тепловые и электрические свойства пористого никеля // Порошковая металлургия. 1972. № 8.
13. Аксенов Г.И., Заббаров Р. О теплофизических константах пористых металлокерамических материалов // Порошковая металлургия. 1967. №6.
14. Кононенко В.И., Барановский В.М., Дущен- ко В.В. Исследование теплопроводности пористого металлокерамического железа // Порошковая металлургия. 1968. №3.
15. Малько П.П., Немченко В.Ф., Львов С.Н., Пугин B.C. Тепло- и электропроводность пористых никеля, железа и стали Х12Р2 // Порошковая металлургия. 1969. №1.
16. Дульнев Г.Н., Заричняк Ю.П. Теплопроводность смесей и композиционных материалов. М., 1974.
17. Шкловский Б.И., Эфрос А.Л. Теория протекания и проводимость сильно неоднородных сред // УФН. 1975. Т. 117. Вып.З.
18. Поляков В.В., Головин А.В. Влияние пористой структуры на упругие характеристики металлов // Изв. РАН. Металлы. 1995. № 4.
19. Киттель Ч. Введение в физику твердого тела. М., 1978.





 CC BY
CC BY 97
97