Моделирование задач гидродинамики Текст научной статьи по специальности «Математика»

Секция вышей математики

■г

ао в? 1?.Э25СЯ7 «ЭН0 6»7 6Э 3 78 0

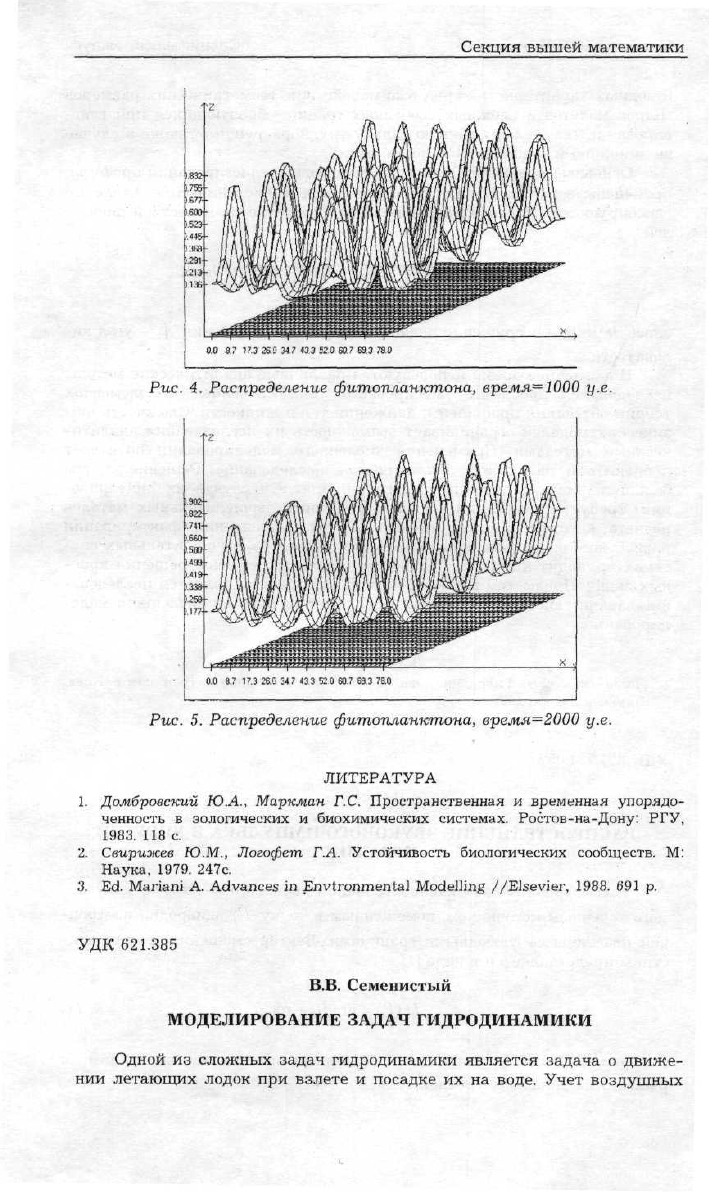
Рис. 4. Распределение фитопланктона, время=1000 у.е.

ЛИТЕРАТУРА

1. Домбровский ЮЛ., Маркман Г.С. Пространственная и временная упорядоченность в эологических и биохимических системах. Ростов-на-Дону: РГУ, 1983. 118 с.

2. Свирижев ЮМ., Логофет Г.А. Устойчивость биологических сообществ. М: Наука. 1979. 247с.

3. Ed. Mariani A. Advances in Environmental Modelling //Elsevier, 1988. 6'91 p.

УДК 621.385

В.В. Семенистый МОДЕЛИРОВАНИЕ ЗАДАЧ ГИДРОДИНАМИКИ

Одной из сложных задач гидродинамики является задача о движении летающих лодок при взлете и посадке их на воде. Учет воздушных

и водных характеристик сред взаимодействия, геометрических размеров гидросамолетов и сложных свободных границ, образующихся при глиссировании тел, делают данную задачу трудноразрешимой даже в случае ее линейной и стационарной постановки.

Основные уравнения, описывающие модель глиссирования профиля, приведены в работе |1]. Так, уравнение для вычисления силы давления глиссирующей плоскокилевой пластины определяется известной формулой:

здесь И и И - погружение редана и скорость погружения, Р - угол ки-леватости. 4

В настоящее время используются различные аналитические методы исследования проблемы глиссирования тел, основанные на элементах теории обтекания профилей и движения тел в жидкости. Сложность физических моделей ограничивает возможность их исследования аналитическими методами. Применение численного моделирования позволяет дополнить и расширить аналитическое исследование. Решение систем большого числа нелинейных уравнений (даже в случае их линеаризации) требует применения новых современных вычислительных методов расчета, к которым можно отнести методы расщепления, факторизации разностного оператора и т.д. Апробация задачи на вычислительных системах приводит к использованию параллельных методов решения краевых задач. Предметом рассмотрения данной работы является исследование задачи глиссирования тела на воде с помощью ее численного моделирования.

ЛИТЕРАТУРА

1. Логвинович Г.В. Гидродинамика течений со свободными границами. Киев: Наукова думка, 1996.

УДК 621.791.052.08

В.Н. Зуев

РАСПРОСТРАНЕНИЕ ЗВУКОВОГО ИМПУЛЬСА В УПРУГОЙ

ПЛАСТИНЕ

Рассмотрена задача распространения звукового импульса, излучаемого точечным источником, помещённым в точку Р0 однородно изотропной пластины со свободными границами. Вектор смещения частиц пластины представляется в виде [1]

где ф и ц/(0.ф.0) - скалярный и векторный потенциалы, являющимися решениями волновых уравнений:

2

и (Р)- gradф+ гсЯ ф,

(1)