Объединение констант взаимодействий Текст научной статьи по специальности «Физика»

Объединение констант взаимодействий Романенко В.А.

Романенко Владимир Алексеевич / Vladimir Alekseevich Romanenko - ведущий инженер-конструктор Нижнесергинский метизно-металлургический завод, г.Ревда

Аннотации: показана методика объединения констант известных взаимодействий, приводящая к размерам пространства-времени, сравнимых с единицами Планка. Полученные размеры объединяются с помощью параболической функции. Дано объяснение возникновения функции с позиций теории времени.

Ключевые слова: взаимодействие, единицы Планка, масштабный фактор, поле великого объединения, теория времени, планкеон.

Keywords: interaction, Planck units, the scale factor, стЫ unified field, theory of time, plankeon.

В настоящее время в Дубне ведутся работы по созданию коллайдера на встречных пучках тяжелых ионов NICA на основе модернизированного сверхпроводящего ускорителя нуклотрона. Основной целью проекта является изучение перехода ядерной материи в кварк-глюонную плазму и смешанной фазы этих состояний. Результаты исследований могут дать информацию о первых этапах эволюции Вселенной.

По мнению автора, первые этапы возникновения Вселенной могут быть описаны теоретическим путем, а именно: на основе объединения констант взаимодействий [1,с.403, 407]. Методике объединения и посвящена данная работа. Сведем все взаимодействия в таблицу:

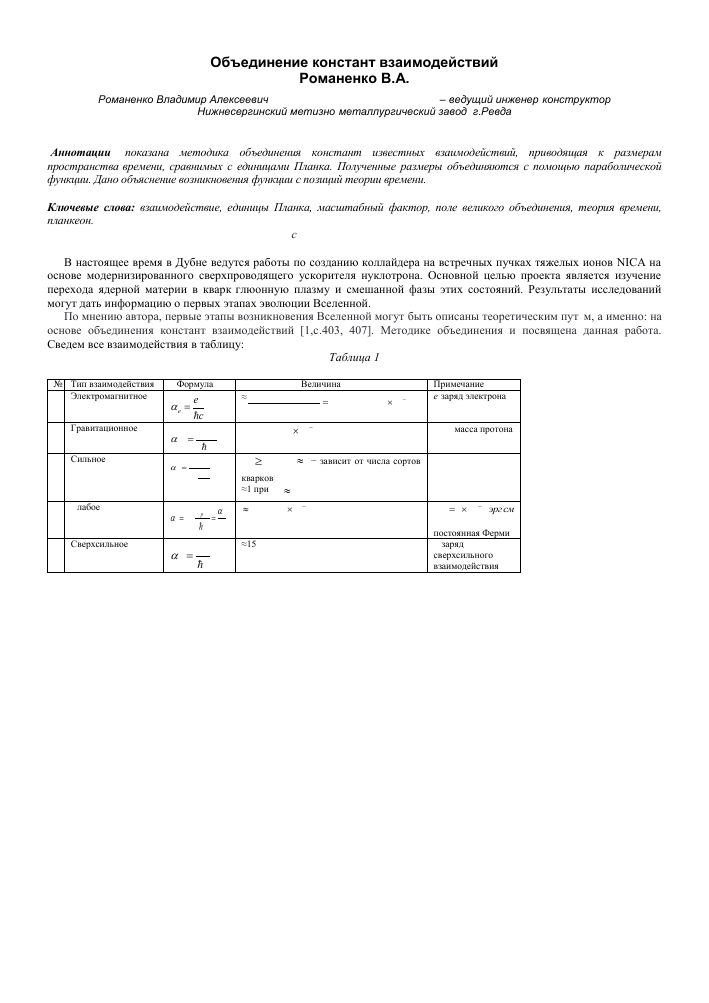
Таблица 1

№ Тип взаимодействия Формула Величина Примечание

1 Электромагнитное е2 ае= — he = 1 , -= 7,2973535308 x 10~3 137,03599911(46) е-заряд электрона

2 Гравитационное mpG agp = hc = 5,9046863 x10~39 m -масса протона

3 Сильное a a =- s , m ln- mp m > mp , a ~ 1 - зависит от числа сортов кварков при m и m

4 Слабое 2 2 a] ~ 1,065028 x 10~5 gj. = lxlü-49 эргсм> постоянная Ферми

5 Сверхсильное a =ML ags hc =15 g-заряд сверхсильного взаимодействия

Будем считать, что все взаимодействия потенциально возникают в кванте Планка, имеющего следующие параметры [2, с.218]:

Gh

• Длина £0 = J—=1,6160456x10 ^;

. время в0 = — = аЩ- »5,3х10~44с; c V c

ich

• масса mo=l— = 2,176828363х10~5г

УУ с^ г С

• плотность р ~ = __~ 5 х к)"3 : температура т = —_и 1032К

"0 л 3 3 0 7

10 и П СМ

где к - постоянная Больцмана.

Из них можно составить следующие комбинации и физические величины:

длина /? _ то° ;

с2

время 0 = —°—;

с3

энергия е0 = т0с2 = Йю0 = — = ^ = 1019ГэВ \

сила F = Ео_ = т0сг = m\G =

L С С G

к

постоянная Дирака п = — = т010с = 1.05459-10 27 эрг ■ сек, 2 л

произведение Йс = т010с2 = то2О; гравитационная постоянная G = 6,672 • 108 дин • см2 / г2.

Для объединения взаимодействий введем дополнительные обозначения для выражения массы Планка через массы электрона - представителя лептонов, и кварка - представителя барионов:

то = тгпг = ткепке (1) где

п - число электронов в массе кванта; пкв - число кварков в массе кванта. Выразим массу протона через массу кварков по формуле: т

тр = 3тке, где т^ =(р) Подставляя в (1), получаем выражение:

тр

то = тРПР (3)

п

где п = —^ число протонов в массе кванта.

р 3

С учетом введенных обозначений преобразуем формулу константы слабого взаимодействия относительно постоянной Ферми:

ас%ъ асфс)2п ссс (т02О)2 Нп2 (аспр2)(т20в2) (4)

&Р — 2 ~ 2 — 2 3 — 4 ПС — 1\ш1дПС

трс тос с

2 С

ПР

где Ыр = асп2р масштабный фактор.

С учетом введенного масштабного фактора формула для слабого взаимодействия преобразуется к виду:

р

где _ _!_ _ тР& _ тР — константа гравитационного взаимодействия для протона.

п2р Ьс т1

Таким образом, масштабный фактор устанавливает величину масштаба между слабым и гравитационным взаимодействиями:

N2 = а = а п 2 (6)

т2 _ ас___„2

■V

а„

№

Свяжем константу слабого взаимодействия с электромагнитным взаимодействием через эмпирическую формулу, приведенную в таблице1:

<£ = (7,2973535308х.р-3)2 =, 028

с 5 5

Определим численное значение масштабного фактора:

=2и _ 1,065028 Х10-5 = |,803699546 Х1033 (8)

г а№ 5,9046863 х10-39 Выразим его через известную длину Планка:

« И «-зз „ 6,1879442 х 10*

£0 1,6160456 х 10 см

Как видим, масштабный фактор близок обратной длине Планка.

Чтобы точно выразить его через эту величину введем экспоненциальную функцию изменения пространственной длины Планка:

1=£0е~ь (9)

и приравняем ее обратной величине масштабного фактора: - _ь [1 см\

1У1Г

Из полученного уравнения находим величину Ь :

( 1Я2 /1/ЛЧ

Ъ = 1п(1,6160456х 1(Г33 х 1,803699546х 1033) = 1п 2,91486075 = 1,069822037 (10)

[1см]

Дадим еще одно выражение, приводящее к масштабному фактору:

сК = «. = 729735308х ^ х 9,1093897х 10'28 = 2,0192073x1033 (11)

г а т 5,9046863 х 10~39 5,5754103х 1025

&р кв

1,6726231 х 10-24 _ /пч

где т = --= 5,5754103х 10-25 г - средняя масса кварка (12)

кв 3

Из полученного выражения находим величину коэффициента пропорциональности: а т 2,0192073 х1033

е=—*--V = --55— = 1,1194806 (13)

аррткв N1 1,8037 х1033

Его можно считать константой сильного взаимодействия (см. табл.1), определяемой по формуле:

е=а =—= 1,1194806 =-1--(14)

1 0,8932714

тр

где т = третъ21Ы = 2,443115331тр.

Таким образом, масштабный фактор может быть записан в виде: 9 а т а п

N2 =-^^ = —^^ (15)

а8ртша, а8рпеа*

Полученные безразмерные соотношения будем называть критериальными уравнениями. На их основе можно составить систему, приводящую к их объединению в единое взаимодействие в пределах планковского кванта длины. Система имеет вид:

к= аепкв =^ = аи2=Ме,(а); = ^ (б) (Щас=^ (в)

' " «в 5

пр =-Кв- (г)

пк 3

Из уравнения (а) находим выражение для количества протонов с учетом (в) и (г): п„ =М = . Ш = N^75 = п, (17)

р Л1 2 ' -у

11 ас \ ае а 3

Из уравнения (а) находим число электронов, используя (17): п _ агПв _ 3 Кц'^5 ^ = ^У5 е аерКа. ае аврЫ„а,

Выражаем квадрат числа электронов через гравитационную константу для электрона:

Я-=4^ = ^ = ^ = (2Д76828363х1°;)У =(2,389653352.10-)-=5,71044314.10- (18) е т20 т О а (9,1093897 х10~28)г2

е е ее ^ ^

Аналогичная константа для протона применена в формуле (5):

= ^ = = — = = (1,301463807-Ю-)2 = 1,69380804-10-

р т2рО трО а№ (1,6726-10-24)г2 ' '

Выражаем гравитационные константы через масштабный фактор:

а_а, V [1 ом]

1 т (аа "1 3^/5

1 ар а]1йе

пр N 5[1ом

-Г I (19)

Зл/5 ) е02

(20)

Как видим, они содержат возрастающую и убьшающую экспоненциальные функции.

1к2 = г,? = 45-1 = —£02 (21)

(ав>а*) [1см\ \УСМ\

где / 2 - пространственная координата, зависящая от возрастающего темпа (правое вращение);

А = 45 а%е - коэффициент;

(а№а*)2

(22)

_ П„.Л _ П„.Л _ «п..л _ М

1к1 = {0е-ь = —§41 см] = -2-[1см] = В[\см\ = ^ (23)

где /к1 - пространственная координата, зависящая от убывающего темпа (левое вращение); В = = = — (24)

ас ^

Как видно из (21), электрон, являющийся представителем лептонов, зарождается в потоке с правым вращением, в то время как протон (см. (23)), являющийся представителем кварков - в потоке с левым вращением. Под потоками следует понимать потоки времени. Умножая (21) на (23), получаем:

1к2 ■ I* = = ¿о = ТТ^Т¿о'В[1см] = А-В-Р\ (25)

[1 см\

Откуда следует связь:

£\=А-В-1\ъш\ = А-В (26)

Рассмотрим отношение обеих координат:

1 ('' р~ь Р 2р~2Ь 1 2

1к\ _ _ е~2Ъ _ к _ 1к1

I ( еъ ( 2 / 2

к2 0

Из него следует:

2 2 2 Щсм] _ В[\см]2 _ 5а _ от3 от/ (27)

1к1 ~10 1~-10 —А----А-----11сМ\ --¿—2-\-1СМ\

А г 2 А т . — ос 9а а „

"2 т, т^п2 а2, -45-

е ge

[1^] " * Путем сложения обеих функций получаем функцию гиперболического косинуса:

Кг Н: = 2{^еЪ+уЪ) = 210сЪЪ =-А-е0 +Щсм] (28)

2 [1 см\

з>

Преобразовываем полученную функцию к квадратному уравнению относительно планковской длины:

е 2 — 1 Л1см\+ — [1см\2 =0 А А

Вводим обозначения длины падающего вектора времени для поля великого объединения:

-т, сЪЪ

с{ои =1ои = —[1см] =

2 2 а„„ а.

45«

[1см] сЬЪ

(30)

и квадрата первой пространственной координаты, полученной выше (см. (23)): Б[1см]2

11 =

3 2

9а2а„„

[1см]

(31)

С учетом введенных обозначений (29) запишется следующим образом:

/2 -от р +72 -о

Откуда

Р2 4- Т 2 Р Т2 т _ VI _ , 1 '

ои - -

2^

о

л

Т.к. /к1 = / , то, подставляя в формулу, получаем:

е+т2

т _ 0 ^ VI

ои — '

2£п

л2 , л2 -26 Ь

¿о + У -е

иг

■ = 1к1екЬ

(33)

- о ^ о

Приравнивая обозначению (30), получаем уравнение:

^и = 1к1СкЪ = [1см]

Из него находим /к1 с учетом (31):

а2 [1см]

скЪ

А

[1см] =

(34)

45а

Из выражения следует формула связи (11.26):

1 = 4АВ или 1 = АВ Запишем в виде (23) и приравняем (32):

В результате вновь приходим к произведению, равному единице, т.е. (26).

Таким образом, имеем двойное представление для / х. Выразим его через константы взаимодействий:

2 2 а а

7 _ £Р д

[1см] а1рад

45а ^А^

[1см]

(35)

Из полученного уравнения находим другое выражение для константы а

где а = 15 есть константа сверхсильного взаимодействия (см. табл.1).

15

. а

аЛ агР

ая К

а

а

(36)

Из (16) находим:

а п ппае а а = 3= 3 —е_

3 а„ п п„ а а.

Л

а

(32)

&е

(37)

а

а.

Оно переходит в первое при а = —— (см. (7)).

с 5

Из (34) находим выражение константы сверхсильного взаимодействия через другие константы:

Л

а^ = а*ае

а

а

Яе

По найденным выражениям (30) и (34) находим численные выражения:

I

«з =

^=^ = ¿^=0,343077126^, (40)

^ = ««{!CM]chb = (5,9046863.Щ-39)2.1,1194806- .$ 44з14 1q44 2g96 =

45« 1 J 45 V '

ge

= 9,032220285 -10= 0,5589087514Í n

С

'-О

А

chb

где chb = 1,62896 для b = 1,0698 из (10).

Т.к. / j < 1, то можно применить тригонометрическую зависимость между /к1 и LGU в виде синуса угла:

А. = sin^= 0,343077126 = 0,613833877 (41)

LOÜ 0,5589087514

( = 37,867° (42)

Этот угол является углом Вайнберга для поля Великого объединения, находимого из условия [3, с.99]:

«М. = sin2 0GU = 3 или sin^GC/=,13 = 0,612372435 (42)

«GU 8 WGU \8

Как видим, углы практически совпадают. Несовпадение можно объяснить недостаточной точностью при эмпирическом определении мировых констант.

По значению квадрата синуса объединим все взаимодействия через поле великого объединения, используя (31) и квадрат (30):

Получаем:

-„ 9 -[1CM] ,999 9

а (а) , / 2 9а а аъ а2452а2 225а а2 а

U/em\4J _ „:-2 а _ \1 _ e ge__ gp s_ge __ge __gs ge

= sln ür.TT =

«i«2 Г, l2

GU Lrrr2 а2 а2 r л . 9а2а а4 аАекЬ2 а2а а2екЬ2 а2а а2екЬ2

GU / gp s Г1 ] e ge gp s e gp s e gp s

[1см] chb)2

45а

«gu

где а = 15 есть константа сверхсильного взаимодействия. Откуда:

а2аа2скЬ2 а2« «а2

«GU = ^F-«em (а) «m (?) (43)

2 ет ^ * ' 2 • 2 п

а а а а 81п ц.,

1 а2а а2 где еНЪ =-, е ^^ . = 1

вт вш а. 2ае

Единичное выражение может быть выражено через гравитационную константу для протона в виде: а 2

а =а —(44)

8Р 2 2

Из формулы можно получить массу протона, выраженную через массу электрона. Для этого следует извлечь квадратный корень из обеих частей:

I- I— а а

,1а =^а или тр = (45)

Из формулы для констант может быть получена формула (38) для а - константы сверхсильного взаимодействия.

Покажем, что область, где возникает поле великого объединения, является областью левой параболы. Для этого

преобразуем уравнение (33):

р2 / 2 р / 2

£ _Ь0~Г1к1 — о | к!

аи 2£0 2 2£0

Если его решить как квадратное относительно £0, то приходим к виду: (£0 — £ги. )2 + /г|2 = (£г;,. )2

(46)

Для данного вьфажения может быть введена координата собственного времени Л'(. = стк . Тогда оно примет вид:

? 2,7 2 г 2 лк ^ VI — ^аи

где -гк=£0- Ьои или 1ои=£0+£к (47)

Введение данной координаты приводит к функции левой параболы, смещенной влево на —

2

^ Г, л /.,1 ^

"ои ~ ~ 2£0 и 2£0 2

= Цю -4 = ^ + (48)

Получение такой функции теоретическим путем может означать создание теории образования вещества и самой Вселенной. Такая теория создана автором. Соответствие теории и экспериментального результата есть критерий истины.

Коротко о теории. Это теория времени. Ее математической основой являются дуальные уравнения двух типов: тангенциальное и синусоидальное. Первое описывает гравитационные явления в континууме и может применяться для изучения областей с евклидовой геометрией пространства-времени, сравнимых с областью Планка. Второе уравнение описывает антигравитационные явления в континууме и может применяться для изучения областей с неевклидовой геометрией пространства-времени, начиная с области Планка. Вывод уравнений производится тремя способами. Первый способ наиболее общий основан на представлении о времени, как скалярном поле. Второй способ основан на одном единственном постулате теории времени. Третий способ приводит к выводу уравнений на основе оригинальной авторской теории вакуума. На основе указанных уравнений и производится вывод параболической функции (48).

Следует отметить, что параболическая функция является лишь промежуточным этапом при изучении природы возникновения Вселенной. С ее помощью описывается геометрическая поверхность кванта Планка, который будем называть планкеоном. Планкеоны являются хроночастицами первого типа, существующими в абсолютной пустоте и являющимися гарантами ее существования. Они представляют из себя «коконы» времени или микро черные дыры. Каждый «кокон» можно рассматривать как субстанцию, состоящую из слоев хрононов и гравитонов, находящихся в силовом равновесии. Известно, что в черной дыре пространство и время меняются местами. В этом случае хрононы, являясь частицами времени, вращаются по окружностям в пространственной плоскости, в центрах которых располагаются гравитоны. Гравитоны являются вакуумными частицами и существуют в обратном времени, что и приводит к притяжению. Планкеон следует рассматривать в виде цилиндра с радиусом и длиной, равной фундаментальной длине Планка. Под действием центробежной и гравитационной сил, происходит внешнее искривление цилиндра в виде левой параболы, описываемой (48). Это искривление приводит к появлению параболической поверхности внутри планкеона. С каждой поверхностью может быть связан свой вектор времени. Оба вектора взаимозависимы и имеют определенные углы и модули в планкеоне. Изучение свойств гравитонов возможно с помощью тангенциального дуального уравнения.

Для того, чтобы планкеон стал нестабильным необходимо, чтобы он встретился с хроночастицей второго типа. В результате контакта происходит временная инверсия гравитонов. Они превращаются в антигравитоны, т.е. частицы, которые начинают движение в прямом направлении времени. Их описание начинает подчиняться синусоидальному дуальному уравнению. Под действием антигравитонов, хрононы начинают переходить с одного уровня на другой с испусканием электромагнитной энергии.

Самым интересным является исследование процессов на первом уровне. Хрононы при переходе на второй уровень, испускают поток тяжелых фотонов. Поток движется в виде винтовой линии по цилиндрической поверхности первого уровня планкеона. Достигнув его временной границы, поток переходит в точки, принадлежащие внутренней параболической поверхности, и отражается в ее фокус в виде двух лучей. Первый луч находится сверху и несет в себе положительную энергию. Второй луч находится снизу и несет в себе отрицательную энергию. В фокусе энергии лучей сливаются, образуя гравитационную энергию, движущуюся в обратном направлении оси собственного времени и достигающую вершины параболической поверхности. Поверхность совпадает с точкой фокуса левой параболы. Поэтому в вершине происходит раздвоение энергии гравитационного потока, и он переходит в виде конуса в отрицательную временную область левой параболы. В этой области поток приобретает свойства поля великого объединения с углом наклона образующей, равной углу Вайнберга. Конический поток, достигнув левой параболической поверхности (48), отражается от нее в виде цилиндрического потока в прямое направление оси времени и достигает поверхности внутренней параболы в двух точках. В точках контакта происходит вновь отражение потока в ее фокус в виде положительной и отрицательной энергий. В фокусе эти энергии переходят в

антигравитационную энергию, которая движется в прямом направлении времени в точку Ь - центра сосредоточения вакуумной энергии внутренней параболы. Новое положение центра связано с переходом возбужденного планкеона на второй уровень.

Рассмотренная картина видоизменения потоков энергий показана на рис.1.

Из рисунка видно, что энергетические лучи, входящие в фокус и выходящие из него в точку Ь , могут рассматриваться как составляющие вектора двух других результирующих векторов. Они входят в точку и выходят из нее под углами Вайнберга для электрослабого поля и показаны зеленым цветом на рисунке.

рис.1. Начало образования материи и времени в планкеоне.

В центре сосредоточения вакуумной энергии слияние энергических лучей приводит к появлению потока хрональной энергии, благодаря которой поддерживается резонансный этап расширения планкеона и происходит рождение основных элементарных частиц, необходимых для образования атомов.

Все вышесказанное закономерным путем вытекает из математической теории времени, примененной к началу образования вселенной.

Литература

1. Акоста В., Кован К., Грэм Б. Основы современной физики. М.: Просвещение, 1981.495с.

2. Климишин. И.А. Релятивистская астрономия. М.: Наука, 1989, 288с.

3. Окунь Л.Б. Элементарное введение в физику элементарных частиц. М, 2006. 128с.