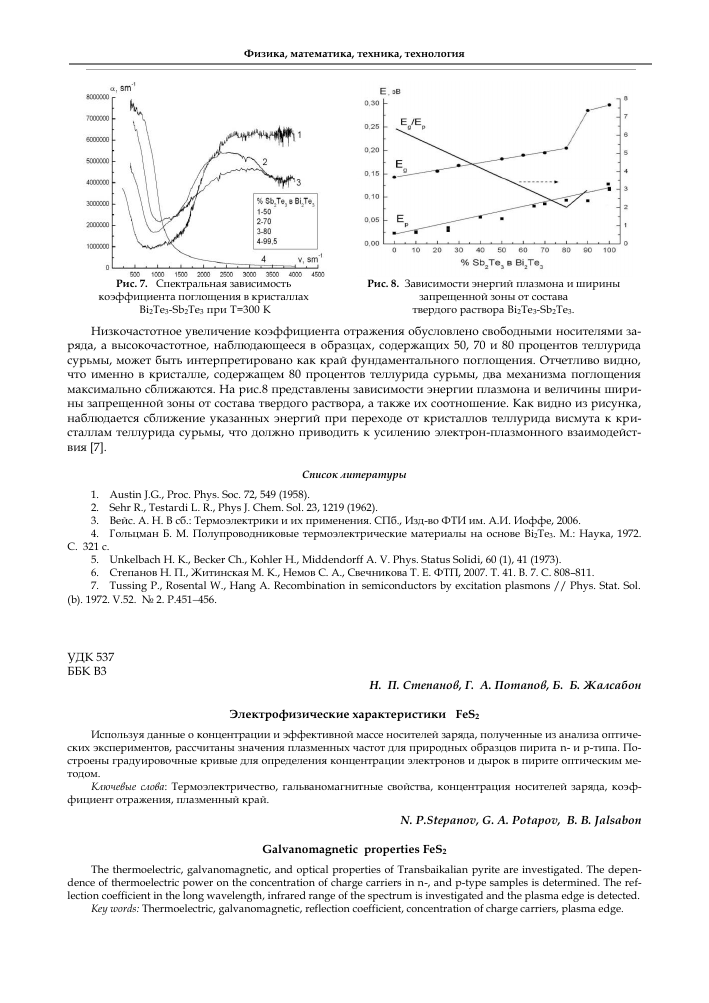
Рис. 7. Спектральная зависимость коэффициента поглощения в кристаллах Bi2Te3-Sb2Te3 при Т=300 К
Рис. 8. Зависимости энергий плазмона и ширины запрещенной зоны от состава твердого раствора Bi2Te3-Sb2Te3.
Низкочастотное увеличение коэффициента отражения обусловлено свободными носителями заряда, а высокочастотное, наблюдающееся в образцах, содержащих 50, 70 и 80 процентов теллурида сурьмы, может быть интерпретировано как край фундаментального поглощения. Отчетливо видно, что именно в кристалле, содержащем 80 процентов теллурида сурьмы, два механизма поглощения максимально сближаются. На рис.8 представлены зависимости энергии плазмона и величины ширины запрещенной зоны от состава твердого раствора, а также их соотношение. Как видно из рисунка, наблюдается сближение указанных энергий при переходе от кристаллов теллурида висмута к кристаллам теллурида сурьмы, что должно приводить к усилению электрон-плазмонного взаимодействия [7].
Список литературы
Austin J.G., Proc. Phys. Soc. 72, 549 (1958).
Sehr R., Testardi L. R., Phys J. Chem. Sol. 23, 1219 (1962).
Вейс. А. Н. В сб.: Термоэлектрики и их применения. СПб., Изд-во ФТИ им. А.И. Иоффе, 2006.
Гольцман Б. М. Полупроводниковые термоэлектрические материалы на основе Bi2Te3. М.: Наука, 1972.
1.
2.
3.
4.
С. 321 с.
5. Unkelbach H. K., Becker Ch., Kohler H., Middendorff A. V. Phys. Status Solidi, 60 (1), 41 (1973).
6. Степанов Н. П., Житинская М. К., Немов С. А., Свечникова Т. Е. ФТП, 2007. Т. 41. В. 7. С. 808-811.
7. Tussing P., Rosental W., Hang A. Recombination in semiconductors by excitation plasmons / / Phys. Stat. Sol. (b). 1972. V.52. № 2. Р.451-456.
УДК 537 ББК В3
Н. П. Степанов, Г. А. Потапов, Б. Б. Жалсабон
Электрофизические характеристики FeS2
Используя данные о концентрации и эффективной массе носителей заряда, полученные из анализа оптических экспериментов, рассчитаны значения плазменных частот для природных образцов пирита n- и р-типа. Построены градуировочные кривые для определения концентрации электронов и дырок в пирите оптическим методом.
Ключевые слова: Термоэлектричество, гальваномагнитные свойства, концентрация носителей заряда, коэффициент отражения, плазменный край.
N. P.Stepanov, G. A. Potapov, B. B. Jalsabon
Galvanomagnetic properties FeS2
The thermoelectric, galvanomagnetic, and optical properties of Transbaikalian pyrite are investigated. The dependence of thermoelectric power on the concentration of charge carriers in n-, and p-type samples is determined. The reflection coefficient in the long wavelength, infrared range of the spectrum is investigated and the plasma edge is detected.
Key words: Thermoelectric, galvanomagnetic, reflection coefficient, concentration of charge carriers, plasma edge.
Параметры электронной системы содержат информацию о генезисе и последующих преобразованиях минералов, определяют их поведение в окислительно-восстановительных условиях земной коры и технологических процессах извлечения [1]. К наиболее важным параметрам электронной системы относят концентрацию свободных носителей заряда, подвижность, эффективную массу, коэффициент термоэдс.
Выбор метода измерения параметров электронной системы обусловлен особенностями пирита БеБг. Наличие неоднородностей и малые размеры выделений минерала позволяют рассматривать оптический метод как наиболее предпочтительный. С другой стороны, определение физических параметров оптическим методом и сопоставление полученных результатов с данными гальваномагнит-ных исследований позволяют получить более надежные значения измеряемых величин.
Цель настоящей работы заключалась в разработке оптического метода определения параметров электронной структуры пирита и сопоставлении результатов с данными электрофизических измерений. Взаимодействие электромагнитного излучения со свободными носителями заряда в большинстве полупроводниковых минералов наблюдается в диапазоне Л>Л0, где Л - длина волны, соответствующая краю собственного поглощения. Поскольку в пирите Лои1 мкм [1], интересующий нас диапазон лежит в средней и дальней инфракрасной (ИК) областях спектра.
В работе [2] проводилось исследование спектров отражения пирита в дальней ИК-области. Авторами наблюдалось сильное изменение коэффициента отражения на частоте v=434см -1, связанное с колебаниями решетки. В работе [3] обнаружен минимум коэффициента отражения И на частоте 276 см-1 и последующий быстрый рост И с увеличением длины волны падающего электромагнитного излучения - плазменный край. Моделирование экспериментального спектра в рамках теории Друде-Лоренца позволило определить резонансные частоты плазменных Vp и решеточных Vph колебаний, а также высокочастотную диэлектрическую проницаемость [3]. Возможность наблюдения плазменного края в пирите позволяет проанализировать возможность определения параметров системы свободных носителей заряда по спектрам отражения ИК-излучения. Для этого необходимо рассмотреть ряд специфических особенностей материала, связанных с типом проводимости в пирите, величиной подвижности носителей заряда и коэффициентом термоэдс.
В литературе имеется большое количество данных об электрических измерениях, выполненных на природных образцах пирита [1, 2, 4]. Пирит встречается в модификациях как п-, так и р-типа [5]. Среднее значение удельного сопротивления пирита р-типа примерно на порядок выше, чем для п-типа, вследствие различной подвижности электронов и дырок [4]. Собственная концентрация носителей при комнатной температуре составляет примерно 21014 см-3 [5]. Из приведенных данных следует, что для пирита выражение, позволяющее рассчитать плазменную частоту колебаний свободных носителей заряда, имеет вид:
{ -кт АТ \
(1)
2 е2 N N
ар = —
п___-_____
* ~ *
, т т .
V п р J
где М и М - концентрации электронов и дырок соответственно, т*п и т*р -эффективные массы, е -заряд электрона, £0 - диэлектрическая постоянная. Для однокомпонентной плазмы однородного образца р-типа выражение (1) можно переписать в виде:
г„---_£ІІ или N¡1 . (2)
ш р *2
^О^т ^О^т тр Є
Современные методы обработки оптических спектров на ЭВМ позволяют с высокой точностью определить плазменную частоту мр и высокочастотную диэлектрическую проницаемость £ж. Таким образом, отношение N^может быть определено с погрешностью, не превышающей 5%. Отсюда
тР
следует, что, опираясь на данные о величине эффективной массы носителей, можно определить их концентрацию. Величину эффективной массы электронов и дырок в пирите можно определить, анализируя данные о подвижности ц. Подвижность дырок при комнатной температуре лежит в пределах 0.5-3 см2/В*с [1]. Такие значения подвижности характерны для локализованных носителей с большой эффективной массой т*п >> т*р. Подвижность электронов в пирите изменяется в широких пределах, однако многие опубликованные значения лежат в интервале 10-50 см2/В*с. Следовательно, эффективные массы электронов в пирите (в приближении одинаковых с дырками времен релаксации) примерно в 25 раз меньше, чем у носителей р-типа. Поскольку концентрация носителей п- и р- типа в пирите может изменяться в широких пределах (1014-1019 см-3), необходимо учитывать дис-
персионную зависимость эффективной массы. Решение подобной задачи путем расчетов на основе известного закона дисперсии носителей представляет определенные трудности даже для хорошо изученных монокристаллических полупроводников. Однако, информация о величине т* и ее дисперсии в природном пирите может быть получена экспериментально.
Для решения этой задачи можно использовать зависимость дифференциальной термоэдс от концентрации носителей заряда. Так, на рис. 1 приведена зависимость величины термоэдс а от хол-ловской концентрации, полученная в лаборатории физики минералов ЗабНИИ, для образцов пирита п- и р- типа. Экспериментальные точки в широком интервале концентраций аппроксимируются прямыми линиями, что указывает на определенную закономерность в изменении электронных параметров материала при смещении уровня химпотенциала как в валентной зоне, так и в зоне проводимости.
Известно теоретическое выражение для расчета коэффициента термоэдс :
'ЯЛ
(3)
где И-постоянная Больцмана, М определяется соотношением (4), О - параметр, зависящий от типа рассеяния носителей заряда [5]. Для рассеяния на акустических колебаниях решетки Q=2, для рассеяния на заряженных дефектах Q=4. Подобные выражения применимы как для локализованных носителей, так и для нелокализованных. В любом случае можно рассчитать эффективную массу носителей заряда, поскольку
(
М = 4п
2тр ЯТ
~~Н2
(4)
где h - постоянная Планка, Т - температура.
Подобный расчет для носителей р-типа представлен в табл. 1. Расчет эффективной массы дырок проводился по формулам (3), (4) с параметром Q=0, что соответствует случаю локализованных носителей, перемещающихся путем перескока (прыжковый тип проводимости). Действительно, полученные в образцах р-типа значения подвижности 0.5-1 см2/В*с указывают на длину свободного пробега 10 Е, что ненамного превышает величину межатомных расстояний в пирите и3 Е. Дифференциальная термоэдс для электронов (п-тип) рассчитывалась по формуле (3) с параметром Q=2, что соответствует рассеянию на акустических колебаниях решетки.
Таблица 1
Термоэдс а и эффективная масса плотности состояний m*/m0 для различных значений концентрации
дырок в p-FeS2
а = I —
е
№ а, мкВ*К-1 N, м-3 т*/т0
1 690 1.02*1023 5.3
2 550 3.2*1024 18.1
3 500 8*1024 22.7
4 460 1.37*1025 23.8
5 400 3.2*1025 26.4
6 350 7*1025 30.2
7 200 1.2*1026 29.5
8 250 2.3*1026 30.8
Используя полученные таким образом данные о концентрации и эффективной массе носителей заряда, а также данные о величине ею, полученные из анализа оптических экспериментов, в соответствии с выражениями (1) и (2), можно рассчитать значение плазменных частот для всех исследованных образцов и построить кривые (рис. 2).
N , м 'Ч 0 ‘‘
Рис. 2. Расчетные значения плазменных частоп в зависимости ^концентрации носителей
для образцов п- и р-типа
Эти кривые в дальнейшем можно использовать как градуировочные для определения концентрации электронов и дырок в пирите оптическим методом при Т=290 К. Например, определим концентрацию носителей заряда в образце пирита, спектр отражения которого подробно анализировался нами в работе [5]. Плазменная частота в этом образце равна 276 см-1 и в соответствии с рис. 2 может принадлежать или электронам с концентрацией п=7*1022 м-3, или электронам с п и 1.5*1025 м-3. Определить тип носителей заряда в образце можно по знаку эффекта Зеебека. Так, исследуемый нами образец оказался однородным с носителями р-типа и, следовательно, концентрация дырок в образце равна 1.5 *1025 м-3.
Данные комплекса электрофизических измерений подвижности, коэффициента термоэдс и хол-ловской концентрации того же образца приведены в табл. 2. Холл-фактор при расчетах был принят равным 1.178, что соответствует рассеянию на акустических фононах. Из приведенных данных видно, что расхождение в значениях концентрации носителей, определенной оптическим и гальваномаг-нитным методами? не превышает « 6%. Таким образом, может быть реализован оптический бесконтактный экспресс-метод определения концентрации свободных носителей заряда в пирите.
Таблица 2
Электрофизические характеристики пирита БеБг
Vph, см-1 Vp, см-1 Є +р N, м-3 ц, а
-п см2В-1с-1 мкВ К-1
434 276 8 + р-тип рср 1,37*1025 0,65 490
Список литературы
1. Воган Д., Крейг Д. Химия сульфидных материалов. М.: Мир, 1981. 565 с.
2. Корсунский М. И., Митриева Н. М., Муратов Э. М. Известия АН КазССР, Серия геологическая. 1969. 6,
11.
3. Степанов Н .П., Тупиков В. М., Лапушков В. М. //Физика земли. 1994. № 1. С. 79.
4. Корсунский М. И., Муратов Э.М. Известия АН КазССР, Серия физ-мат. 1970. № 6. С. 63.
5. Шуй Р. Г. Полупроводниковые рудные материалы. Л.: Недра, 1979. 288 с.





 CC BY
CC BY 88
88